|
STUDI DI BIOCLIMATICA |
||||||||||||||||||||
|
|
|
STUDI DI BIOCLIMATICA |
||||||||||||||||||||
|
|
|
La rappresentazione in
proiezione ortogonale dell'ombra portata da un segmento |A-B|
su di un piano orizzontale, alle ore solari t, si
effettua immaginando che per il segmento |A-B| passi un
piano g ortogonale al piano orizzontale e
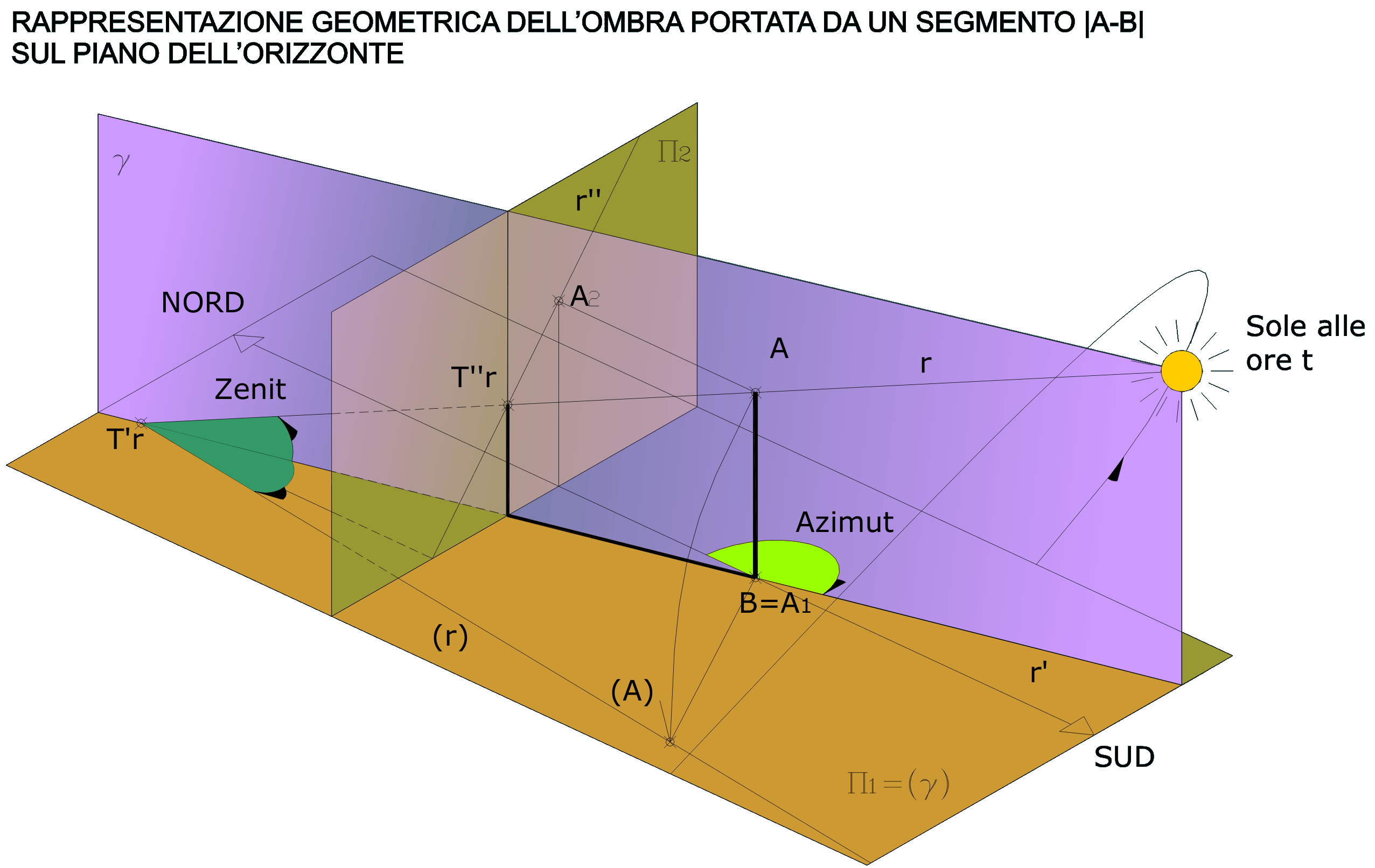
contenente il raggio proiettante r. Il piano g contiene, fra le infinite rette proiettanti e parallele ad r, quella passante per il punto A in direzione alla sorgente luminosa, e, dovendo passare per il segmento |A-B|, ortogonale al piano dell'orizzonte, rimane univocamente determinata la sua posizione nello spazio. Nota la distanza del segmento |A-B|, come quota del punto A = A2 = qA, si ribalta il piano g sul piano orizzontale, ruotando in un verso stabilito lungo la traccia del piano = r'(prima immagine di r) in (g), poichè le distanze e gli angoli si conservano sul ribaltamento di (g) si ha: qA = (qA ribaltato) ortogonale ad r', r = (r ribaltato) passante per T'r = (T'r). La rappresentazione piana di (r), nota r' e (A), del raggio proiettante r si determina facendo passare per (A) una retta inclinata rispetto ad r' dell'angolo zenitale. L'intersezione della retta (r) per (A) con r' determina la prima traccia della retta r =T'r. Nota la T'r si risale a r'' (seconda immagine di r) e a T''r (seconda traccia della retta r). La T''r rappresenta l'intersezione del raggio proiettante r, passante per A, con un piano verticale contenente r'' passante per A2 (seconda immagine di A). esempio animato |
 |
